In recent years, engine manufacturers have strived to increase engine efficiency to reduce fuel consumption and emissions, for competitiveness and to meet strict government regulations. These advancements have led to highly stressed engine parts, in particular the crankshaft hydrodynamic bearings.
Hydrodynamic bearings are thin film bearings that rely on a film of lubricant (oil or air) to create a clearance between the moving and stationary bearing surfaces. Hydrodynamic bearings are commonly used in engines, turbines, generators, compressors, gearboxes and pumps in the automotive, aerospace, power generation, oil and gas and chemical processing industries to transfer loads from the rotating components to the stationary casings.
There are two types of hydrodynamic bearings: journal bearings and thrust bearings. Journal bearings transfer radial loads, whereas thrust bearings transfer axial loads.
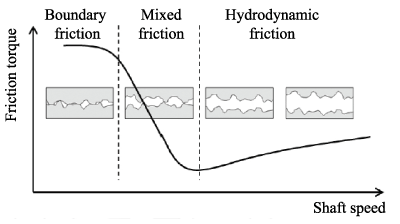
Hydrodynamic bearings operate in the boundary layer, and in mixed or hydrodynamic lubrication regimes. In the hydrodynamic lubrication regime, the fluid film thickness exceeds the combined roughness of the surfaces, such that the two bearing surfaces are completely separated by a film of lubricant. Typically, the fluid film thickness in the hydrodynamic lubrication regime is extremely small, in the order of micrometers, much smaller than the other dimensions of the bearing.
In the mixed lubrication regime, the fluid film thickness is less than the combined roughness of the surfaces. Metal-to-metal asperity contact occurs in combination with the hydrodynamic pressure of the lubricant. Surface roughness significantly affects the performance of the bearing in this regime. If the oil film increases further, the system will transition into the hydrodynamic lubrication regime.
The bearing friction coefficient is at a minimum in the transition between the hydrodynamic lubrication and mixed lubrication regimes, see Figure 1. Hence, it is beneficial to operate bearings in this transition, but unfortunately due to the metal-to-metal contact, wear and durability problems may occur. To design bearings that operate in the transition, engine manufacturers must perform a detailed analysis of the complex bearing behavior under a wide range of operating conditions. High load in the engine deforms the components elastically, therefore elastic deformation needs to be considered in the simulation and a fluid-structure interaction analysis is required.
Figure 1 Stribeck curve for different lubrication regimes [1]
Modeling fluid flow in thin-film bearings with Navier-Stokes fluid elements is not practical. The Navier-Stokes elements requires many layers of elements through the film thickness, making the analysis expensive. Moreover, Navier-Stokes fluid elements tend to be unstable for thin films, especially in fluid-structure interaction problems where the film thickness varies during the solution.
Fluid flow in thin-film bearings can be accurately solved using Reynolds’ equation. The Reynolds equation is derived from the Navier-Stokes equations using the below assumptions:
- The variation of pressure across the fluid film is negligible.
- The film thickness is much smaller than the length in the flow dimension.
- Viscous forms dominate inertia forces.
The ADINA System has Reynolds-based fluid elements. In this Tech Brief, we show how the ADINA Reynolds-based fluid elements can be used to reliably and accurately solve mixed elasto-hydrodynamic lubrication problems.
ADINA Reynolds-Based Fluid Elements
The ADINA Reynolds-based fluid elements can be used to reliably solve fluid flows in thin films, for example, hydrodynamic bearings, lubricant films between pistons and cylinder heads, thin channel flows, fluid films between human joints, etc.
The ADINA Reynolds-based fluid elements solve the Reynolds equation, which has the above three Reynolds assumptions embedded in the formulation. As such, only 1 layer of Reynolds-based fluid elements is required to accurately solve the thin film flow. Moreover, the Reynolds-based elements are extremely stable for thin film flow, such that far fewer iterations are required as compared to using Navier-Stokes fluid elements.
The ADINA Reynolds-based fluid elements can be directly connected to Navier-Stokes fluid elements. In this way, Navier-Stokes fluid elements can be used in the large fluid domain region, for example, the bearing reservoir that feeds the thin fluid film, and Reynolds-based fluid elements can be used in the thin-film regions, where the large fluid domain and the thin-film domain are directly connected.
The ADINA Reynolds-based fluid elements can be used in pure CFD analysis, and fluid-structure interaction (FSI) analysis. Non-Newtonian fluid material models can be applied to the ADINA Reynolds-based fluid elements, which is important for mixed elasto-hydrodynamic lubrication problems, as the lubricants show a strong non-Newtonian behavior, where the lubricant’s viscosity increases strongly at high hydrodynamic pressures. Thermal effects also change the lubricant’s viscosity and need to be considered in the simulation.
The ADINA Reynolds-based fluid elements can be used for smooth boundary flow (pure hydrodynamic lubrication regime) and for rough boundary flow (mixed lubrication regime). For rough boundaries, the ADINA Reynolds-based elements solve an enhanced Reynolds equation based on the Patir-Cheng model [2], [3].
In the Patir-Cheng model, the effects of surface roughness of partially lubricated contact are derived using an average flow model. The average flow model is based on empirical pressure and shear flow factors, so that the average lubricant flow can be expressed in terms of the flow factors and the mean quantities such as the mean pressure and nominal film thickness. Then, an average Reynolds equation governing the mean pressure is derived in terms of these flow factors. The flow factors are obtained from statistical models of randomly generated surface roughness, or from measured surface roughness values.
Journal Bearing under an Eccentric Displacement
A good verification problem for hydrodynamic analysis, is the classical problem of a journal bearing under an eccentric displacement for which there is an analytical solution [4]. The problem is described in Figure 2.
Figure 2 Schematic of journal bearing problem
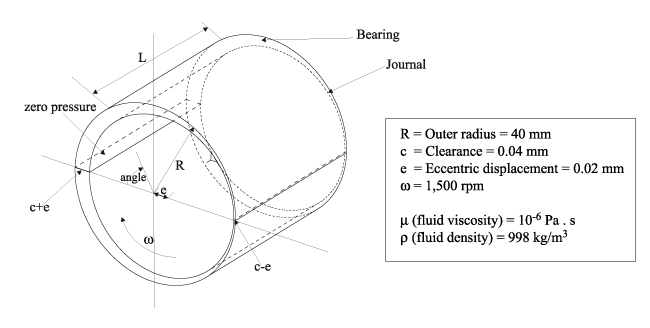
In this problem, the inner shaft rotates at a constant angular velocity and the outer shaft is stationary. An eccentric displacement, e, is applied to the inner shaft. The pressure distribution and velocity distribution over the journal surface is to be calculated.
Figure 3 shows the analytical and ADINA Reynolds-based element solutions for smooth boundaries. As can be seen, the ADINA solution exactly matches the analytical solution.
(a) Pressure distribution over the journal surface
(b) Velocity distribution over the journal surface
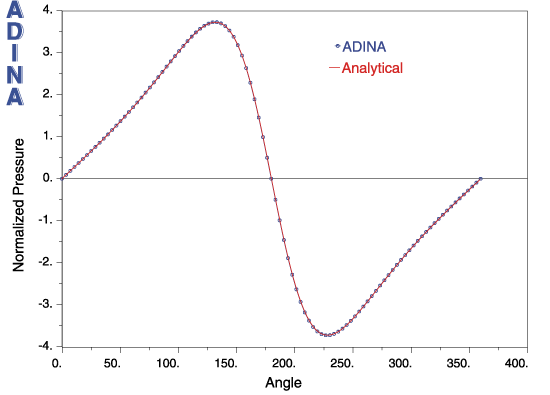
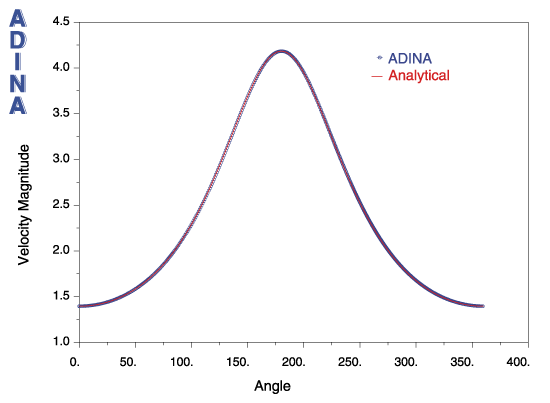
Figure 3 Solution for smooth boundaries (no cavitation)
Next the mixed lubrication solution with rough boundaries is considered. In this problem, the fluid film thickness is assumed less than the combined roughness of the surfaces, such that the asperity contact occurs which affects the solution.
In ADINA, the Patir-Cheng model is used to compute the mixed lubrication solution for rough boundaries.
In this model, the local film thickness, hT, is defined to be of the form:
hT = Ī“1 + Ī“2
where Ī“1 and Ī“2 are the random roughness amplitudes of the surfaces measured from their mean levels; h (see Figure 4) is the nominal film thickness defined as the distance between the mean levels of the two surfaces. It is assumed that Ī“1 and Ī“2 have a Gaussian distribution of heights with zero mean and standard deviations Ļ1 and Ļ2, respectively.
Figure 4 Film thickness function used in the Patir-Cheng model for rough surfaces
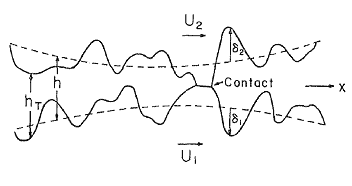
Figure 5 shows the solution when only the moving boundary (inner shaft) is rough (Ļ1 = 0, Ļ2 > 0) and when only the stationary boundary (outer shaft) is rough (Ļ1 > 0, Ļ2 = 0), as compared to the smooth boundary solution. As expected, the flow is accelerated if the moving boundary is rough, and the flow is decelerated if the stationary boundary is rough.
Figure 5 Solution for rough boundaries (no cavitation)
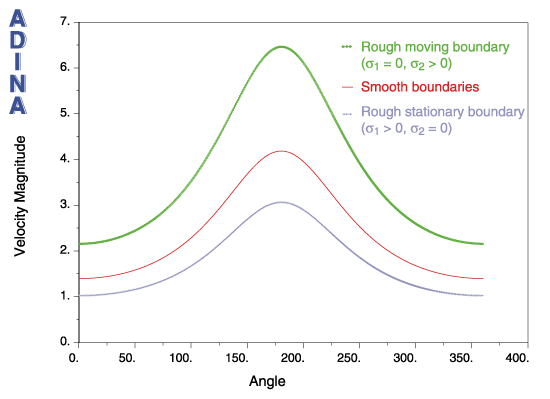
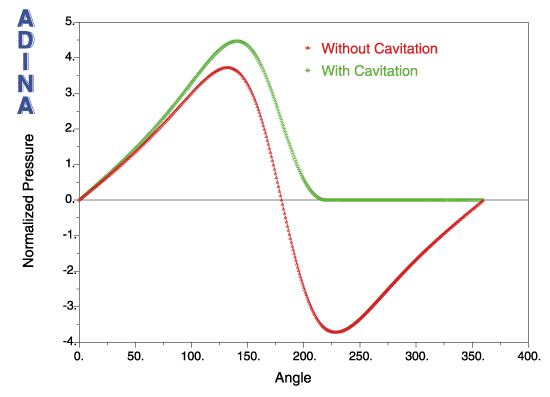
Figure 3a shows negative pressure over half the journal surface. Cavitation occurs if the pressure is lower than the vapor pressure. If the liquid lubricant cavitates, small vapor-filled cavities form in the low-pressure region. These cavities will then collapse as the lubricant moves to the high-pressure region, generating small shockwaves, which leads to cyclic stresses and fatigue failure from the repeated implosions. Cavitation plays a critical role and is a common cause of failure in journal bearings.
The ADINA Reynolds-based fluid elements can be used together with a cavitation model. Figure 6 shows the pressure solution for the journal bearing problem for smooth boundaries with and without cavitation. As can be seen, the pressure distribution is substantially changed when cavitation occurs. With cavitation the low-pressure is limited to the vapor pressure (which is zero in this example), and the high pressure is slightly increased. As the pressure distribution is changed, the resulting uplift of the journal bearing for a given eccentric displacement is also changed.
Figure 6 Pressure distribution for smooth boundaries with cavitation
Equilibrium of a Rotating Shaft
In the next example, we consider the equilibrium of a rotating shaft supported by a hydrodynamic journal bearing proposed by Friswell et al. in the book āDynamics of Rotating machinesā, Section 5.5, [5].
Figure 7 describes the problem. In the problem, the shaft rotates at a constant angular velocity. The shaft is initially concentric with the bearing. As time progresses, the center of the shaft moves until it settles in an equilibrium position which is to be calculated. In the equilibrium position, the weight of the shaft is balanced by the hydrodynamic force generated by the thin film of the journal bearing. This is a transient fluid-structure interaction (FSI) problem. The ADINA Reynolds-based fluid elements with a cavitation model are used to model the flow in the thin film of the journal bearing.
Figure 7 Equilibrium of a rotating shaft
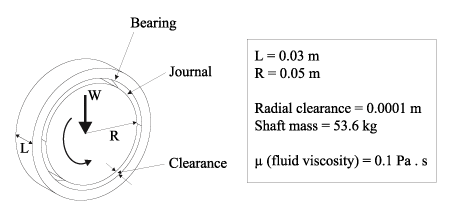
Figure 8 shows the time history evolution of the position of the center of the shaft when the shaft rotates at 1,000 rpm. As can be seen, the shaft moves downward and to the right before settling into its equilibrium position.
Figure 8 Time history evolution of the center of the shaft
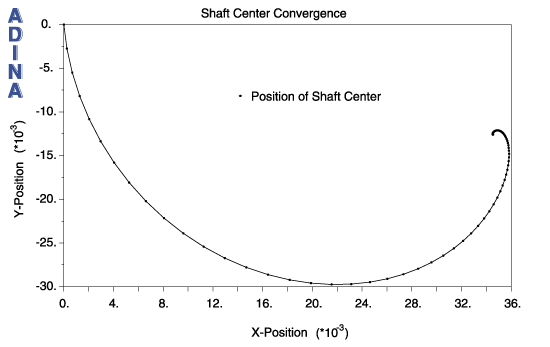
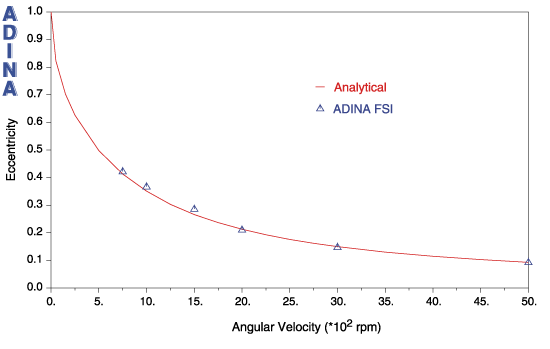
Figure 9 compares the ADINA FSI solution with the analytical solution given in [5] for different shaft angular velocities. As can be seen, the ADINA solutions closely match the analytical solutions. The eccentricity is defined as the ratio of the magnitude of shaft displacement to the radial clearance.
Figure 9 Equilibrium solutions for different shaft angular velocities
Conclusion
This Tech Brief demonstrates how the ADINA Reynolds-based fluid elements can be used to model the flow of thin lubricant films. These fluid elements are formulated using the Reynolds equation for smooth and rough boundaries, and can be used to provide more reliable, accurate and efficient solutions than obtained using Navier-Stokes fluid elements for thin lubricant films.
The ADINA Reynolds-based fluid elements are powerful, and strengthen the ADINA offering for complex fluid-structure interaction problems.
Keywords:
Thin film flow, lubricant films, Reynolds-based elements, Reynolds equation, cavitation, journal bearings, thrust bearings, hydrodynamic bearings, fluid-structure interaction
References
- D. Sander, H. Allmaier, H. Priebsch, M. Witt, A. Skiadas, āSimulation of journal bearing friction in severe mixed lubrication ā validation and effect of surface smoothing due to running-inā, Tribology International, 96 (2016) 173-183
- Nadir Patir and H. S. Cheng, āAn Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubricationā, Journal of Lubrication Technology, 100 (1978) 14-17
- Nadir Patir and H. S. Cheng, āApplication of Average Flow Model to Lubrication Between Rough Sliding Surfacesā, Journal of Lubrication Technology, 101 (1979) 220-229
- Ronald L. Panton, Incompressible Flow, 4th Edition, Wiley, ISBN-10: 9781118013434
- M.I. Friswell, J.E.T. Penny, S.D. Garvey and A.W. Lees, Dynamics of Rotating Machines, Cambridge University Press, 2010
