An earthquake can cause a dam to crack or dislocate, or even cause its component blocks to detach. The damage can result in uncontrolled water release or a catastrophic flood. Numerical methods such as finite element analysis play an important role in assessing the possible seismic damage to dams. In this blog post, we show how ADINA was used by a team of engineers in Switzerland for this challenging task.
Dam Safety in an Earthquake
The roof considered is the wide-span steel structure shown in Figure 1. The circular dome shown in the middle has a diameter of 80 m and is 16 m high. The dome is supported at its rim by transitional trusses that connect to the surrounding structure. The small circled zone on the rim of the dome shows the area of interest for which laboratory test results were obtained, see Figures 2 and 3.
The dam considered is the Gigerwald dam in the Canton of St. Gallen, Switzerland, see Figure 1. It is a 147m-high arch dam comprising 24 vertical monoliths (blocks) made of concrete. An arch dam is designed in a way that the water pressure and self-weight cause compression, also between the monoliths, thereby preventing them from separating.
Swiss regulations required that the dam should not allow uncontrolled release of water for an earthquake of 8.0 MSK intensity at its location, with a return period of 10,000 years. To this effect, the design team used ADINA’s linear and nonlinear dynamic analysis capabilities, modelling the contact between blocks, to evaluate the performance of the dam and tightness between the blocks when under a seismic event of this nature.
Dam type: Double-curvature arch dam
Number of blocks: 24
Max height: 147m
Crest length: 430m
Dam thickness: 7.0m (crest) to 22m (base)
Figure 1: The Gigerwald dam.
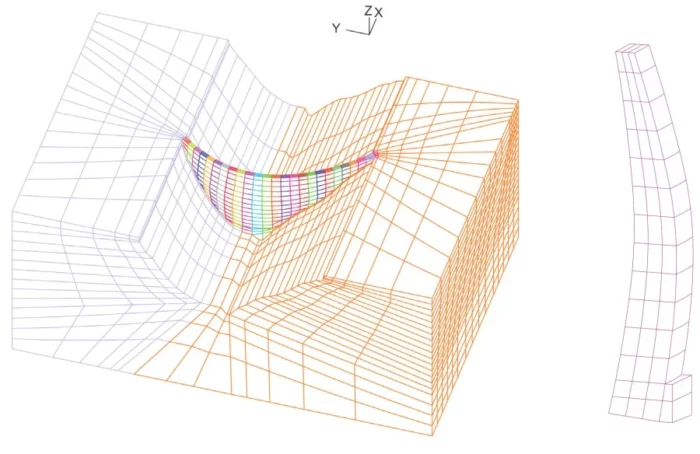
The ADINA model of the dam is shown in Figure 2. Seismic shaking was applied in the ADINA model as acceleration loading. The seismic load was applied in combination with the dam’s self-weight and the reservoir water pressure on the upstream side of the dam. The hydrodynamic effects were included as well in the dynamic analysis.
Figure 2: Finite element model of the dam. (Left)The dam and the rock base.
(Right) Detail of a central monolith, no. 11, of the dam.
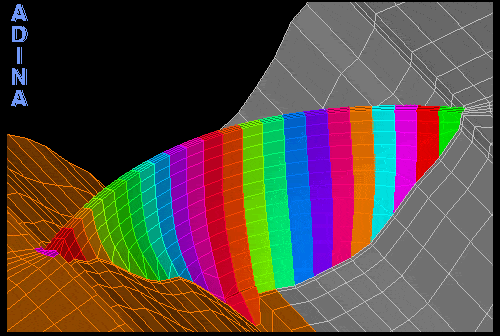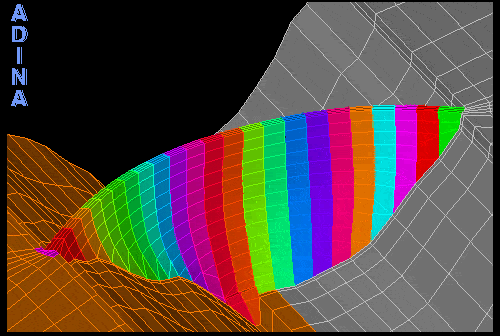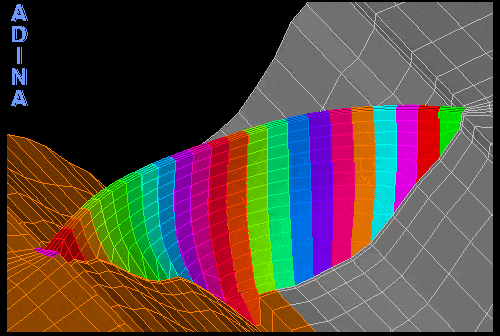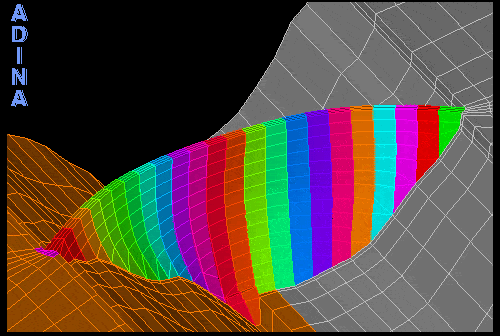
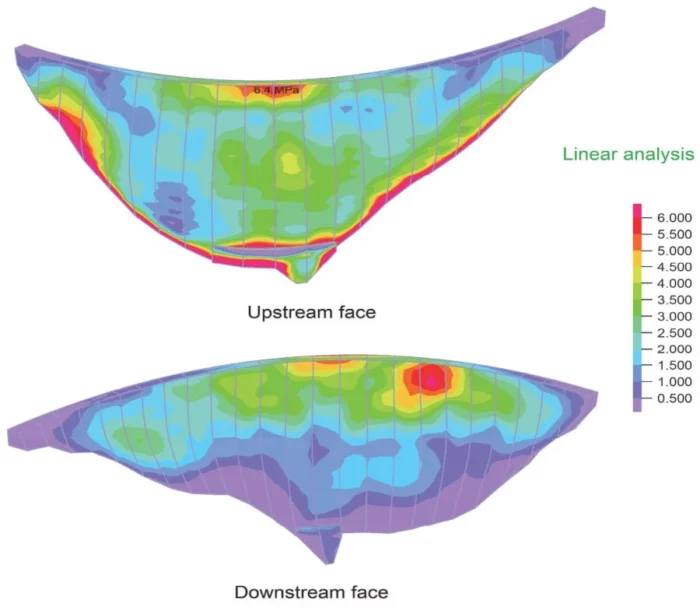
The engineers first conducted a linear dynamic analysis to determine if the blocks might separate during an earthquake of the prescribed magnitude. In this analysis, the dam was modeled as a single piece consisting of monoliths that are glued together. The results showed that the maximum tensile stress might indeed exceed the separation limit, and therefore the monoliths would be very likely to separate (see Figure 3). As can be seen, the represented maximum principal stresses (predominantly tensile) are continuous across the dam’s body and between the individual monoliths.
Figure 3: Principal tensile stresses obtained from linear dynamic analysis.
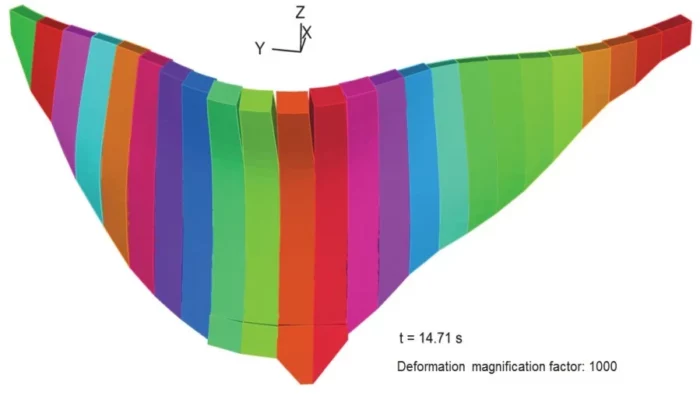
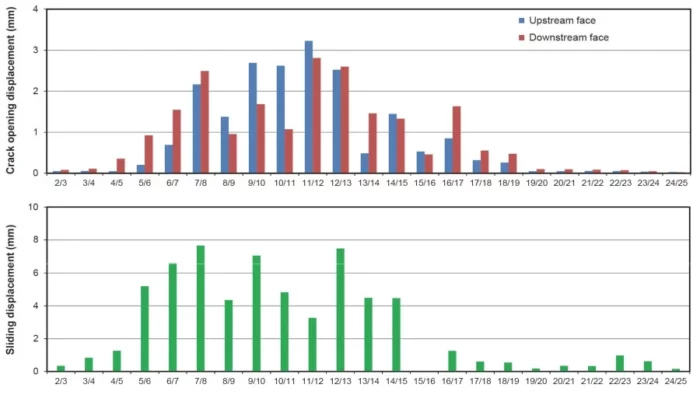
To determine whether this separation might pose a safety threat, a nonlinear dynamic analysis was conducted. For this analysis, contact was defined between the touching faces of adjacent monoliths. The results showed that the maximum separation and sliding displacements would occur at the crest level of the dam. The separations are in the order of several millimeters (see Figure 4 and Figure 5).
Figure 4: Block separation under earthquake shaking. Note that the deformation is magnified by 1000 times.
Figure 5: Maximum opening and sliding displacements between monoliths at crest level.
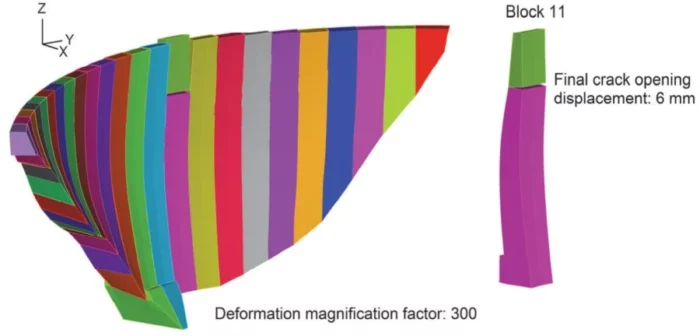
When blocks separate from each other at crest level, the arch-dam compressive effect is lost, and some of the monoliths may start to act in cantilever over a free vertical length at their top. It becomes possible that the upper portion of a monolith may be fully detached from its rest due to fracture if the earthquake-induced horizontal forces are too large. The engineers evaluated this possibility using a 3D model with several pre-existing horizontal cracks whose locations were informed by the previous analyses. The results showed that the final crack opening and the movement of the detached portion are within the safety margins. For example, when the assumed crack is 27 meters below the crest level (the highest vertical tensile stress occurs at this point), the crack opening is 6 millimeters.
Figure 6: Deformation of the dam with detached upper portion in certain monolith.
From the results of these extensive analyses, the engineers concluded that the dam would be safe during an earthquake of the magnitude prescribed by the local authorities.
This application demonstrates just a few of the powerful features of ADINA that make it an ideal tool for solving structural problems. In particular, it is seen that a complex nonlinear analysis including contact using the same finite element discretization, if necessary, can be directly carried out after a linear analysis.
Reference
- S. Malla, “Comparison between 2D and 3D analyses of seismic stability of detached blocks in an arch dam,” Proceedings of the Second European Conference on Earthquake Engineering and Seismology, Istanbul, Aug. 25-29, 2014.
Courtesy of Dr. S. Malla, Axpo Power AG, Switzerland