Point in Polygon Test in GenerativeComponents

The Point in Polygon test helps in determining if a given point lies inside a given polygon. For the sake of simplicity, we assume the polygon to be 2D planer.

Final Result

This video demonstrates the point in polygon test results

Solution

There are many algorithms to achieve this. However, here, we will use Ray-Casting algorithm. We chose this algorithm due to its simplicity. For example, first, we project a ray in a fixed direction (here, positive X-direction). 

Then we determine the test result based on the number of times the ray intersect with the given polygon:

When number of intersection is 0

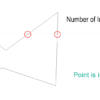
When number of intersection is even

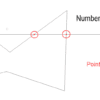
When number of intersection is odd

Implementation

First, we create a custom global function in GCScript. 

Then, for the ray, we use a line of a large length. This line is along the positive X-Direction.

And finally, to test the intersection of this line and the given polygon, we use the AtCurveCurveIntersection technique of point node.

Code

bool PointInPolygon(Point TestingPoint, ICurve TestingPolygon, CoordinateSystem CS)
//Check if a Point is inside a Polygon or Not
{ 
    Line l= new Line(); 
    l.ByStartPointDirectionLength(TestingPoint, CS.XDirection, Pow(2,32)); 
    Point Ipt= new Point(); 
    Ipt.AtCurveCurveIntersection(TestingPolygon, l, null, null, false); 
    if (Ipt.Success)       //Intersection check 
        { 
            if (Ipt.Count%2!=0 || Ipt.Count==0)     //Point inside polygon check 
            { 
                return  true; 
            } 
            else 
            { 
                return false; 
            } 
        } 
        else 
        { 
            return false; 
        } 
}

Limitations

This algorithm is simple, but it does not give correct result in the following cases:

1. The point lies in the boundary or on a vertex of the polygon.
2. There is an edge parallel to X-axis, it might happen it the casted ray overlap with this polygon edge.
3. The magnitude of X -Range of the polygon is greater than 2³² units.

Further Scope of Work

Further, you can try to make corrections in the algorithm to overcome the above limitations. For example, you can solve Limitation 2 by casting the Ray in directions other than X or Y axes.