Choose Area of Interest
SEARCH SOFTWARE
Bridges are lifelines, and aging infrastructure poses a significant challenge. Bridges connect communities, enable commerce, and ensure critical services can reach those in need. When these lifelines falter, the impact is felt deeply, from school routes to emergency response times....

by Oana Crisan
Digital twin workflows rely on precise reality capture software, accurate 3D reconstruction, and scalable infrastructure modeling tools to reflect real-world conditions. While mesh models have powered visualization for years, they limit fidelity—especially for fine geometry, transparency, and lighting. To overcome...

by Aude Camus
Infrastructure professionals across transportation, energy, water, and cities need modern CAD software to design, model, and deliver projects faster, smarter, and with greater context. Meeting these demands requires smarter, more connected ways of thinking about design, data, and delivery. With...
by Alan O’Grady
In the complex world of infrastructure, where sustainable design and digital innovation intersect, stories of successful project delivery often hinge not just on the software used, but on the individuals who master it. We recently spoke with Andrew Germain, an...
by Alan O’Grady
For Nicolai Nolle, CEO of Viscan GmbH, the goal was to deliver a high-accuracy digital twin for infrastructure construction—capturing and updating site conditions daily using advanced reality capture workflows. They were the digital backbone for the B29 highway expansion, a...

by Aude Camus
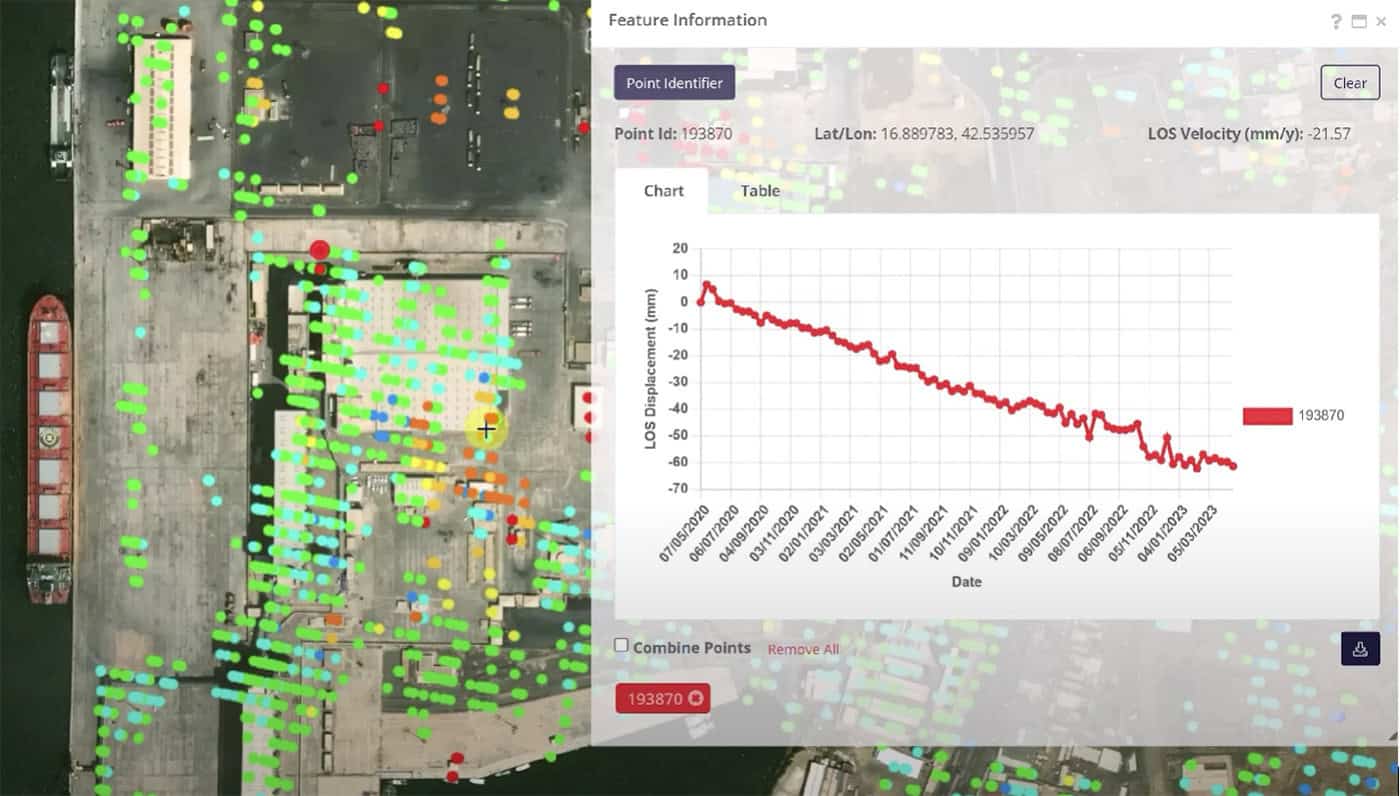
Seismic rehabilitation of creeping ground using a sustainable micropiled PT raft Organization: GeoStruxer Location: Jazan, Saudi Arabia Project phase: Completed and operational Estimated project cost: USD 5.4 million with a 2.1 million cost savings from optimization Bentley software: PLAXIS, RAM...
by Edita Kemzuraite
by Breda Kiely
Are You Buying Effort or Value? Rethinking Transportation Resilience. Ask 10 people in transportation what “resilience” means, and you’ll likely get ten different answers. And that’s exactly the point: resilience isn’t one thing. It includes people, data, systems, contracts, materials,...
by Amy Heffner
Imagine a workflow as dynamic as the world you’re capturing. A process where your tools don’t dictate your path but adapt to your project’s unique demands. As an engineer, surveyor, or planner, you don’t just capture data; you create the...

by Aude Camus