I read a lot of reports and serve as a peer reviewer for a number of journals. I am continuously amazed by the number of otherwise smart engineers and scientists that mess up significant figures in their writing.
Back in the day when we used slide rules, it was necessary to be cognizant of significant digits. But with the advent of computers, it became possible to store and report numerical values with the number of digits far beyond the precision of the measurement or equation used. It is then up to the author to report values with the correct precision.
For example, a pressure sensor in a SCADA system may measure pressure with the precision of two digits (e.g., 62 psi). However, the SCADA system may convert the analog reading to a number with many more digits (e.g., 62.861298) most of which are meaningless and confusing.
The principle is simple. Report the number of digits that you know is correct. Leading and trailing zeros can be troublesome. 0.007 has one significant digit. But 54.6000 has 6. The number of trailing zeros depends on the precision of the measurement. Integers should generally be treated as having an infinite number of trailing zeros. The integer 2 is really 2.0000000_. Zeros between significant digits are significant (e.g., 0.405 is 0.405).
Writers working with large numbers often feel compelled to display digits beyond a reasonable level. For example, they may want to report a pressure as 27,871 psf, when only the first two digits are meaningful. Two solutions to this are to use a more reasonable unit such as converting that value to 190 psi. The other option is to scientific notation and report 28 x 103 psf.
Problems often crop up when people do math with numerical values. The rules for addition and subtraction are simple, the results should have no more significant figures than the least precise value used. For example, let’s add
4.676
3.9
2.8712
0.0021
11.44932
No. The answer is 11.4.
For multiplication and division, the number of significant figures is the fewest number of digits in the operands. For example,
0.021 x 45.6675 is not 0.95902 but 0.96. Leading zeros are not significant.
When eliminating digits, is it best to round up or down? I sometimes struggle with what to do when the first insignificant digit is a 5. It doesn’t matter much because the first insignificant value doesn’t matter. However, it is better to round 5 up to the next higher last digit.
There are two fundamental properties at work here that folks should have learned in high school—accuracy vs. precision. Precision refers to the original measuring tool’s reported results and how close multiple readings of the same phenomena are to one another, while accuracy refers to how close the numerical value is to the true value. Data can be accurate but imprecise; precise but inaccurate; both or neither.
Ideally, measurements should be reported with an indication of the precision of the value such as 656 +/- 6 gpm and those values should be carried through their calculations. However, this would get very messy for most applications.
When writing or reviewing your next document, keep these rules in mind and the final product will look more professional and better convey the meaning of the data.
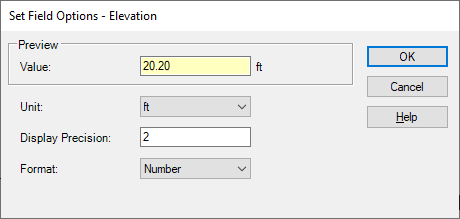
In Bentley’s OpenFlows software, the user can control the display precision of any value. Simply right-click on the property and select “Units and Formatting”.
You can then modify the units, the display precision, and the format (number, scientific, general—20.20, 2.02e+01, 20).
Happy calculating!
P.S. If you are interested in a webinar on using modeling and field data for anomaly detection, you may want to look into this upcoming webinar.
You can then modify the units, the display precision, and the format (number, scientific, general—20.20, 2.02e+01, 20).
Happy calculating!
P.S. If you are interested in a webinar on using modeling and field data for anomaly detection, you may want to look into this upcoming webinar.
Want to learn more from our resident water and wastewater expert? Join the Dr. Tom Walski Newsletter today!
