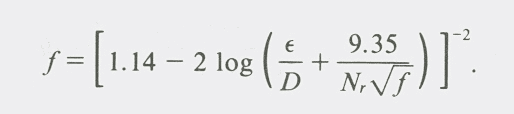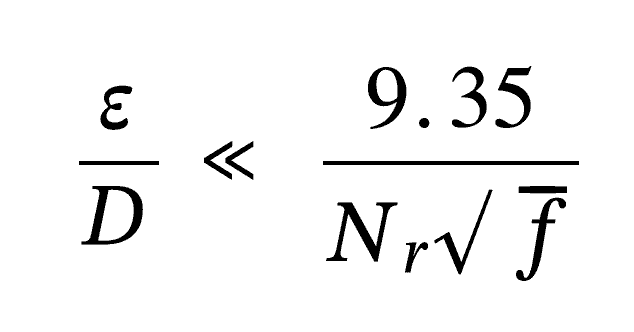The title of this blog comes from a question asked by one of our Bentley OpenFlows users. If the temperature of water in a pipe changes, does head loss and flow change?
Like most questions in hydraulics (and life), the answer is, “It depends.”
In this particular case, changes in flow depend on changes in viscosity, and such changes will only matter if viscosity is important.
If you look at the Moody diagram or Colebrook-White equation, you’ll see that viscosity (and hence Reynolds number) only matters in certain flow regimes depending on what’s happening in the boundary layer.
The overall governing equation is the Colebrook-White equation (or one of its approximations). As the Reynolds number or roughness becomes larger, the importance of viscosity becomes smaller. We can look at two extreme cases.
Where f = friction factor, ε = roughness height, D = diameter, Nr = Reynolds number
Case 1. Very rough pipes at high Reynolds numbers (upper right corner of Moody diagram). In this case the viscosity doesn’t matter and lines in the Moody diagram are flat. Therefore, the friction factor (f) in the Darcy-Weisbach equation is constant. The answer to the original question is therefore that, under this theory, water temperature doesn’t matter (unless it turns to ice).
Case 2. Hydraulically smooth pipes with relatively low Reynolds number (bottom of Moody diagram). In this case, the friction factor (f) depends to some extent on the temperature which affects the kinematic viscosity. While the Colebrook-White equation covers the compete range from smooth to rough conditions, let’s look at the extreme case of very smooth pipes, which can be described by the Blaius equation.
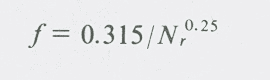
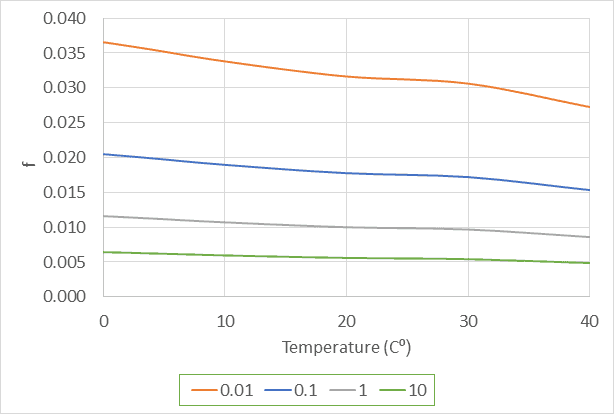
In this case, the friction factor (f) depends on the velocity, pipe size and kinematic viscosity (i.e., temperature). I separated the effect of the temperature from that of the velocity and diameter in the Reynolds number and came up with the following graph.
The different lines correspond to different values of VD, with V (in m/s) and D (in m). For example, the orange line would correspond to slow velocity in a small pipe (e.g., 0.1 m/s in a 0.1 m pipe = 0.01) while 10 would be a high velocity in a large pipe (e.g., 5 m/s in a 2 m pipe = 10).
In this smooth flow case, the friction factor (f) and head at a given flow decreases as the temperature increases. If the temperature varies over a wide range, this variation can make a difference. For example, if VD = 0.1, the head loss can decrease by 16% in going from near freezing to 40 C⁰. Because flow varies as the square root of head loss, this could mean about a 4% change in flow. In most water and wastewater systems, the temperature doesn’t vary by that much.
Case 2, however, is a fairly extreme case with very smooth pipe and a large variation in temperature. Most water distribution system piping falls in the transition zone between Case 1 (rough) and Case 2 (smooth). For practical purposes, variations in temperature and viscosity don’t matter much.
What about people who want to use equations like Hazen-Williams and Manning or similar equations? There is no term in these equations to account for viscosity and changes in viscosity. The implication is that changes in viscosity don’t matter. Many years ago, I played around with possible adjustments to Hazen-Williams C-factors based on parameters like velocity and viscosity. In general, the effects were negligible except for the case where there are large changes in velocity for very rough pipes. But that’s a subject for another blog.
How can someone determine if viscosity changes are important? Look at the Colebrook-White equation above.
If
Then viscosity does matter.
Keen observers will note that they don’t know the friction factor (f) when they try to use this relationship. We’re talking orders of magnitude here so they can make a reasonable initial estimate of the friction factor (f).
So, unless you are dealing with small flows in small, very smooth pipes with very large changes in temperature (and viscosity), you don’t need to worry much about the contents of this blog.
If you want to contact me (Tom), you can email [email protected].
Want to learn more from our resident water and wastewater expert? Join the Dr. Tom Walski Newsletter today!