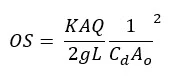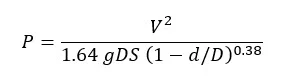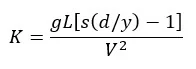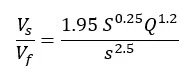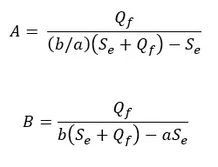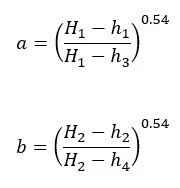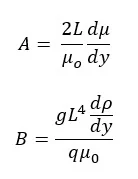I’ve had a long love affair with dimensionless numbers. In hydraulics in particular and transport phenomena in general, dimensionless numbers help us characterize the kinds of systems we’re working with. Most hydraulics problems are so complicated that putting them into a classification based on dimensionless numbers helps us understand what is important and what isn’t.
In my work in water and wastewater hydraulics, the two that show up most of the time are the Reynolds number and Froude number. A small Reynolds number indicates that viscous forces dominate, while a large value says that inertial forces dominate. A large Froude number indicates rapid flow, while a small number points to tranquil flow.
But there are many other useful dimensionless numbers. Some others I’ve run into include the Peclet, Prandtl, Rayleigh, Schmidt, and Sherwood numbers. I once had a chart that listed dimensionless numbers, and there are many of them. The Darcy-Weisbach friction factor is also dimensionless, although it’s not usually lumped in with other dimensionless numbers. The Manning coefficient and Hazen-Williams C-factor are sometimes thought of as dimensionless, although they have some weird units.
When I worked for the Corps of Engineers in Vicksburg, Mississippi, I lived down the street from a guy named Garbis Keulegan. He worked in the hydraulics lab, and he was about 90 years old at the time. I only talked with him once, but I later learned that there was a Keulegan Number concerning the relative importance of inertia and drag forces on a solid in wave dynamics. That’s probably the closest I’ll ever get to a real dimensionless number. I wish I had realized what an important guy he was and gotten to know him better.
When I’m working on a problem, I try to reduce it to its dimensionless form, and frequently a dimensionless number drops out. Over the years, I’ve come up with a handful of dimensionless numbers. While they shed light on the problem, I don’t think any of them are significant enough to ever become a “Walski number.” I was reminiscing about some of the dimensionless numbers I’ve developed. Here’s a summary of a few of them.
Water Leakage
Are flows from water leaks controlled more by the size of the leak or the resistance that comes from the soil? We did a bunch of testing, and I came up with this number characterizing the importance of the orifice vs. the soil (Walski et al., 2006).
Where OS = orifice:soil number, K = hydraulic conductivity of soil, A = cross sectional area of soil, Q = flow, L = length of flow path, Cd = orifice discharge coefficient, Ao = orifice opening area.
Gas Pockets in Sewer Force Mains
I worked on a real system problem where hydrogen sulfide pockets were eating away at sewer force mains. I wanted to find places where hydrogen sulfide was being carried along with the flow as opposed to where it collected and damaged pipes. We did some follow-up work at Wilkes University (Walski et al., 1994) and came up with the following number.
When P > 1, the gas pocket would move downstream. This can help identify where corrosion problems are likely to occur. It has worked in practice.
Large Solids Transport in Sewers
A similar problem exists in solids transport in sewers and other open channels. When the solids are completely submerged in the flow, then tractive force theory works well to predict movement because both weight, drag, and buoyancy forces act on the entire solid. However, when the solid is partly submerged, weight (gravity) acts on the entire solid, but buoyancy and drag act only on the submerged portion. We did two separate projects on this for steady (Walski et al., 2009) and unsteady flow (Walski et al., 2011) and found that movement could be predicted by
Where K = solids movement number, L = characteristic length of solid, s = specific gravity of solid, d = depth of flow, y = height of solid, V = velocity
The portion in brackets could be described as a buoyancy number, while the rest of the number could be considered a solids Froude number. As the value became small, the solid would move. The results differed from the traditional tractive force analysis. Traditionally, to increase the likelihood of movement, the slope could be increased, but for large solids, as the slope increased, the depth of flow decreased which could offset the slope effect.
In the unsteady study, we found that the water actually moved faster than the solids, thus resulting in unsteady conditions. The ratio of solid vs. fluid velocity could be given by the unsteady
This equation was more empirical than the others, since the coefficient 1.95 depended on the units. In the above equation, Q is in L/s.
Water Distribution Model Calibration
In the early days of model calibration, there was debate over whether it was better to adjust pipe roughness or demand to achieve model calibration. When you only tested the model at a single flow rate, you couldn’t tell which to adjust, and you could force calibration by compensating errors. I realized that you needed to collect data under different flow conditions to understand the source of the discrepancy between the model and field data. The easiest way to do this was to conduct hydrant flow tests. I was able to derive dimensionless correction factors for demands and pipe roughness (C-factor) which would indicate whether the discrepancies in the model were due to demands or hydraulics. The two correct factors were
Where Qf = fire hydrant flow, Se = initial estimate of demand
Where
Where H1 = HGL at source during normal demand, H2 = HGL at source during flow test, h1 = measured HGL at flow test location for normal demand, h2 = measured HGL at flow test location for hydrant flow test, h3 = model estimate of HGL at flow test location for normal demand, h4 = model estimate of HGL at flow test location during hydrant flow tests.
A is a correction factor for demands while B is a correction factor for C. When A = 1, the model demands are correct; A > 1, demands should be increased; A < 1, demands should be decreased. When B = 1, C is correct; B > 1, C should be increased, B < 1, C should be deceased a is an indicator of model accuracy during normal conditions, while b is an indicator of model accuracy during flow test.
Viscosity Stratified Flow
I first got into the power of dimensionless numbers in my Ph.D. research with the Corps of Engineers at the Waterways Experiment Station (Walski, 1979). I was looking at the flow to a weir or slot (selective withdrawal) for a fluid where the viscosity varied with depth. Starting with the laterally average 2D Navier-Stokes equation, I was able to simplify them down to two dimensionless numbers
Where μ = viscosity, L = characteristic length, y = elevation, ρ = density, q = flow per unit width
A is simply an indicator of the magnitude of the viscosity gradient, while B is the density gradient relative to the viscosity. It turned out that for naturally occurring stratification due to temperature or salinity, viscosity gradients have little effect on velocity profiles. But in the lab, I was able to create viscosity gradients using either sugar or carboxy methyl cellulose, where viscosity gradients have a significant effect. The most significant effects were when I extended this into non-Newtonian fluids like dredged material, which is where this project started (Walski, 1980). But I didn’t come up with any dimensionless numbers for that case.
If anyone wants to see a copy of any of the papers I’ve mentioned, let me know at [email protected].
Summary
I’ll admit that none of my dimensionless numbers changed the world. But the ability to take the multiple parameters that describe a problem and boil them down to one or two dimensionless numbers makes it easier to get a handle on a problem. My affection for dimensionless numbers I’ve known and loved continues.
References:
Walski, T., 1979, Viscosity Stratified Flow to a Line Sink, Waterway Experiment Station Technical Report EL-79-6 and Ph.D. Dissertation, Vanderbilt University.
Walski, T., 1980, “Prediction of Velocity Profile in Fluid Which Yield Stress Varies with Depth,” Journal of Rheology, 24:6, 741-753.
Walski, T., 1983, “Technique for Calibrating Network Models,” Journal of Water Resources Planning and Management, 109:4, 360-371.
Walski, T., Barnhart, T., Driscoll, J. and Yencha, R., 1994, “Hydraulics of Corrosive Gas Pockets in Force Mains,” Water Environment Research, 66, 772-778.
Walski, T., Bezts, W., Posluszny, E., Weir, M. and Whitman, B., 2006, “Modeling Leakage Reduction Through Pressure Control” J. AWWA, 98:4, 147-155.
Walski, T., Edwards, B., Helfer, E. and Whitman, B., 2009, “Transport of Large Solids in Sewer Pipes,” Water Environment Research, 81, 709-714.
Walski, T., Falco, J., McAloon, M. and Whitman, B., 2011, “Transport of Large Solids in Unsteady Flow in Sewers,” Urban Water Journal, 8:3, 179.187, doi.org/10.1080/1573062X.2011.581298.
If you like blogs like this, you can go back to our library of blogs at https://blog.bentley.com/category/hydraulics-and-hydrology/.
Want to learn more from our resident water and wastewater expert?
Join the Dr. Tom Walski Newsletter today!