One of the main functions of sewers is to move solids. Simply moving the liquid phase while leaving the solids behind would not be satisfactory. The calculations of whether flow in a sewer is adequate to move solids are governed by tractive force design. (Actually, “tractive force” is not a force but a shear stress usually referred to as tractive stress or tractive tension.)
Tractive Stress
Tractive stress is calculated as
τ=pgRS
Where τ= tractive stress, lb/ft2, Pa; ρ = density pf fluid, lb/ft3, kg/m3; g = acceleration due to gravity, ft/sec2, m/s2; R = hydraulic radius, ft, m, S = slope of channel
This is discussed on our book, Wastewater Collection System Modeling and Design (Walski, et al., 2004). (LaVere Merritt from Brigham Young wrote the section of the book on tractive stress.)
The actual tractive stress calculated above is compared with the required minimum tractive stress to determine if a particular solid will move. As the solids become larger and their specific gravity increases, the needed tractive stress to move them increases. There are numerous formulas in the literature that can be used to determine required tractive stress. Mercifully, those calculations have been converted into tables and graphs that engineers can use to determine the minimum slope of a sewer to move solids (ASCE, 2007).
Usually, sand grain particles are used as the benchmark for determining required tractive stress because of their high specific gravity. If the flow can move sand grains, it should be able to move most sanitary solids which have a much lower specific gravity. The theory relies on the fact that the sand grains are completely submerged in the flow, which for sand grains is fairly easy to achieve. Bentley’s SewerGEMS calculates the available tractive stress for use in sewer design and compares that value with the minimum required tractive stress.
Large Solids
But what happens when you need to move large solids. For this blog, we’ll call “large solids” those that are taller than the depth of flow. Any part of the solid above the water level contributes to the weight of the solid but not to its buoyancy.
We did a series of experiments at Wilkes University and developed some theoretical expressions to determine when large solids would be moved by the flow (Walski et al., 2009). We came up with a dimensionless solids buoyancy number that would indicate the likelihood that a large solid that would move in a pipe.
![]() , for d > y
, for d > y
Where SG = specific gravity of solid, d = height of solid, mm, y = depth of flow, mm
As the specific gravity increases or the depth decreases, it becomes more difficult to move the solids.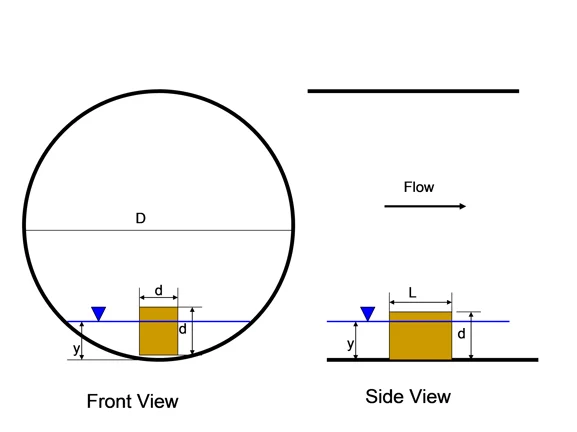
Definition sketch
Here’s what the experimental setup looked like.

Experimental setup
And the results looked like this. The solids Froude number is V2/gL where L is the length of the solid.
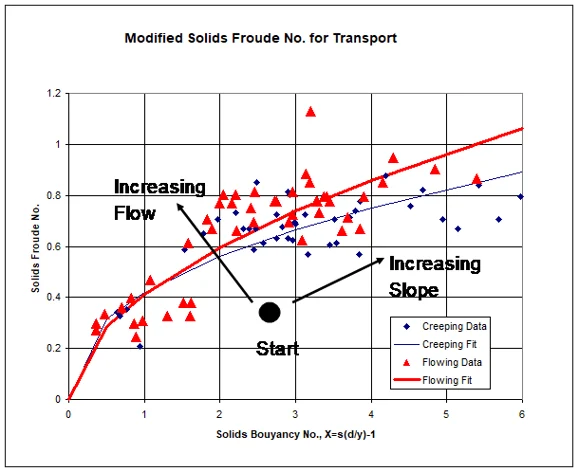
Results for steady flow
The interesting point about large solids is that, unlike smaller solids, as you increase the slope, you don’t increase the likelihood that the solid will move. This is due to the fact that when the slope increases, the depth of flow decreases.
The above approach works well for flows that are relatively steady. But what about the flow in the upper reaches of a collection system where the flow comes in pulses (e.g. shower, toilet flush, washing machine load) and can be zero much of the time. In that case it’s necessary to study pulsed flow on solids movement.
We conducted a second project (Walski et al., 2011). As expected with pulsed flow, the liquid phase of the flow tends to “outrun” the solids, leaving them behind after a pulse to be picked up on the next pulse. We found that the relative speed of the liquid and solid phase in our experiments could be given by
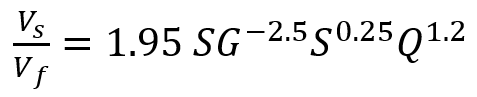
Where Vs is the velocity of the solid, m/s and Vf is the velocity of the fluid, m/s
However, this equation was developed for 4-inch (100) mm pipe with flows mostly around 4.5 L/s. It may not be accurate outside of that condition. The figure below shows how a solid moves through pulsed flow.
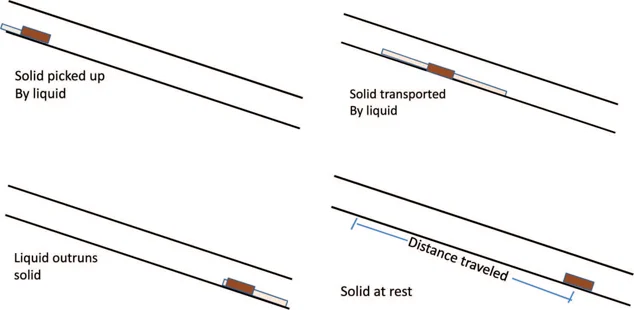
Illustration of large solids transport by liquid phase
The figure below shows that the solid moved 35 m in 90 seconds while the liquid moved 55 m.
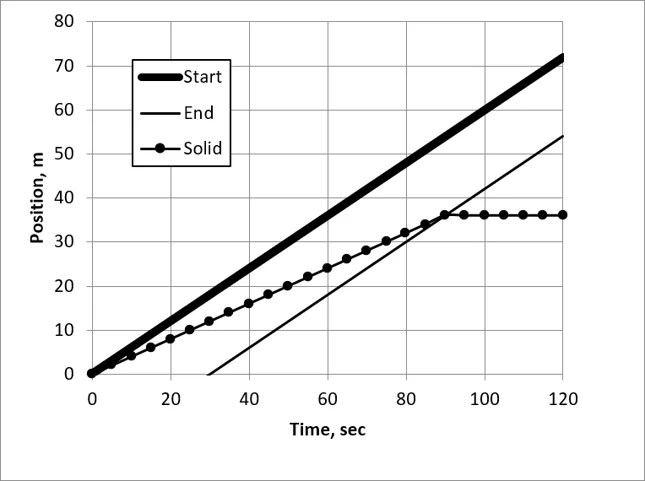
Movement of a solid during a liquid pulse
We had fun watching all sorts of solids move through our experiment (rags, disposable diapers, feminine hygiene products, chocolate candy bars). The good news is that most of these items have a low specific gravity and tend to move easily.
The best paper on this topic was one by Penn et al. (2019). Roni Penn actually used human feces for some of her experimental work. (I’m not ready to get my hands dirty with that.) There are several methods for making artificial feces on the web, and one that is actually patented (Qin and Marsh, 2012).
In general, sanitary sewers should not have much of a problem with large solids (unless they get trapped in grease balls) as most common large solids have a specific gravity near one. Plus it is not easy to get them into sewers. Combined sewers are a bigger problem in that these items can get in through storm inlets and lay in the bottom of the sewer until the next storm.
To get more in depth information on this topic see:
ASCE, 2007, Gravity Sanitary Sewer Design, ASCE Manual of Practice 60, Reston, Va. (and WEF Manual of Practice FD-5, Alexandria, Va.).
Penn R., Maurer, .M, Michalec, F., Scheidegger, A., Zhou, J., Holzner, M., 2019, “Quantifying physical disintegration of faeces in sewers: Stochastic model and flow reactor experiments,” Water Research, 152: 159-170, doi:10.1016/j.watres.2018.12.037.
Qin, W. and Marsh, R., 2012, Artificial Feces, US Patent O252042.
Walski, T., Edwards, B., Helfer, E. and Whitman, B., 2009, “Transport of Large Solids in Sewer Pipes,” Water Environment Research, 81:709, doi:10.2175/106143009X407465.
Walski, T., Falco, J., McAloon, M. and Whitman, B. 2011, “Transport of Large Solids in Unsteady Flow in Sewers,” Urban Water Journal, 8:3, 179-187, doi:10.1080/1573062X.2011.581298.
Walski, T., Barnard, T., Harold, E., Merritt, L., Walker, N. and Whitman, B., 2004, Wastewater Collection System Modeling and Design, Bentley Systems, Exton, Pa.
If you want to look up past blogs, go to https://blog.bentley.com/category/hydraulics-and-hydrology/. And if you want to contact me (Tom), you can email tom.walski@bentley.com.
Want to learn more from our resident water and wastewater expert?
Join the Dr. Tom Walski Newsletter today!