This blog is part of a guest learner series, and written by Dr. Ian Fisher, Ph.D. Dr. Fisher is an adjunct professor at the Western Sydney University Water Group in Sydney, Australia. For a preliminary discussion, please email: [email protected] or [email protected].
Why Model Chlorine Concentrations Accurately in Distribution Systems?
Water utilities are required to achieve effective chlorination by maintaining a detectable free chlorine concentration to the system extremities. The initial dose required to inactivate pathogens may subsequently completely react with chemical contaminants remaining after treatment but before the water reaches these extremities. Then, either the initial dose must be increased, or booster doses are required at intermediate locations.
A cost-effective chlorination strategy is the least-cost combination of doses (locations and rates) that achieves effective chlorination for a given stable flow regime and water temperature. Searching for such a strategy requires extended-period simulations for many dosing location and rate combinations.
It is therefore imperative that any model of chlorine concentrations used to assess the cost-effectiveness of chlorination accurately predicts whether chlorine is below detection (<0.2 mg/L is often assumed) before the water reaches the extremities.
A similarly large number of simulations are needed to find a strategy for any other flow/temperature scenario (e.g., for winter instead of summer). Consequently, the model must also be efficient because the user does not need to derive new coefficient values whenever a new trial set of temperatures, initial/booster doses, or flows are to be simulated.
Why is the Traditional Chlorine Bulk-Decay Model Inadequate?
The widely used model of chlorine decay with one constant bulk decay coefficient (and one wall-reaction coefficient) is inadequate for this purpose, on both counts:
- It does not accurately represent the shape of even a single decay curve, commencing from the dose applied in a decay test
- The coefficient must be re-derived (preferably from lab decay tests) for each different trial initial dose, booster dose, and temperature
- It cannot represent chlorine concentrations resulting from mixing multiple sources of water of dissimilar quality
- It cannot accurately represent the formation of harmful by-products (e.g., trihalomethanes), the limitation of which is now an additional effectiveness criterion in many countries.
These inadequacies arise from regarding the decrease in free chlorine concentration as “decay;” i.e., a function only of chlorine. The same is true for any other such model (all of those in EPANET).
Overcoming these problems requires a paradigm shift. Think in terms of chlorine reactions, in which reaction rate is proportional to the concentration of both chlorine and the substances it reacts with (the reactants). Even if all reactants are lumped together as one substance, we still have two species to simulate, i.e., we must use a multi-species model, which is available as MSX in Bentley’s OpenFlows WaterGEMS and OpenFlows WaterCAD software.
What is the Simplest Chlorine-Reaction Model with Sufficient Accuracy and Efficiency?
It turns out that the reactants must be split into at least two groups (fast and slow reactants) to obtain sufficiently accurate predictions of chlorine concentrations from a reaction model. This is embodied in the two-reactant (2R) bulk-reaction model. Although it has four coefficients (two initial reactant concentrations and their respective decay coefficients), these are all derived from one pair of lab decay tests conducted at a specific temperature.
In deriving 2R models for over one hundred different waters, we have yet to find a case for which more than two reactant groups are needed to accurately represent bulk decay within the full operational range of initial doses and up to three booster doses. In all cases, a single set of the four coefficient values accurately described all decay test data for a single water, thus satisfying the desired efficiency criterion.
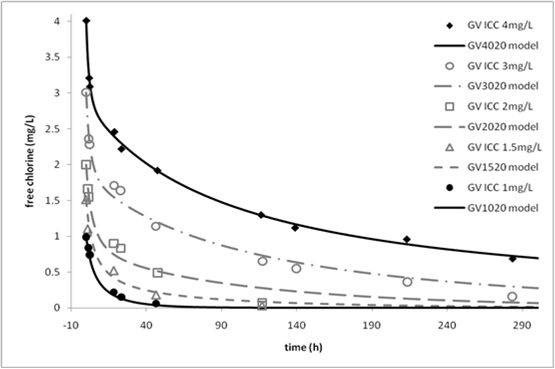
Figure 1 shows a comparison of decay-test data for water from Greenvale, Australia with predictions from the 2R model after deriving its four coefficients from only the data of the highest and lowest initial chlorine concentrations (ICCs). See Fisher et al. (2011) for further details and examples.
The four coefficient values used to generate these predictions from the 2R model are used in the MSX setup example given in the next section.
Figure 1. Comparison of decay-test data (points) at 20°C for Greenvale water with 2R model predictions (curves). Only filled points were used for model calibration.
Incorporating the 2R Model in MSX (in OpenFlows WaterGEMS or OpenFlows WaterCAD)
Navigate to Edit Multiple Species Analysis setup to configure the 2R model (for details, see https://bentleysystems.service-now.com/community?id=kb_article_view&sysparm_article=KB0015266.
Specify the 2R model using the following input file keywords and formats (Table 1). The four coefficient values (KF, KS, F0, and S0) are for water from Greenvale, Australia.
[TITLE]
Two-reactant (2R) model of chlorine decay in bulk water at a single temperature (Fisher et al. 2011)
[OPTIONS]
.
.
[SPECIES]
; Type Name Units
BULK FCL MG/L ; Free chlorine concentration
BULK F MG/L ; Fast reactant concentration (mg Cl-equivalent/L)
BULK S MG/L ; Slow reactant concentration (mg Cl-equivalent/L)
[COEFFICIENTS]
; Type Name Value
CONSTANT TC 20 ; Document water temperature [degC] (not used)
CONSTANT KF 0.141 ; Fast rate coefficient at TC [L/mg/h]
CONSTANT KS 0.00366 ; Slow rate coefficient at TC [L/mg/h]
[PIPES]
; Type Name Expression
RATE RF -KF * FCL * F ; Fast reactant decay rate with chlorine
RATE RS -KS * FCL * S ; Slow reactant decay rate with chlorine
RATE RCL RF + RS ; Rate of chlorine reaction (decay)
[QUALITY]
; Initial concentrations at source node 1
;Type Species ID Concentration Units
NODE FCL 1 3.0 MG/L
NODE F 1 1.13 MG/L
NODE S 1 2.87 MG/L
Table 1. A 2R bulk chlorine-reaction model in MSX format
Prediction of Chlorine Concentrations at Any Temperature: the 2RA Model
The 2R model has also been augmented (forming the 2RA model) to account for the effect of temperature on reaction rate using the Arrhenius relationship. One additional coefficient (EOR) is required, which is also derived from the decay tests used to obtain the original four coefficients. However, at least one additional decay test must be conducted at a different temperature from the original pair to provide the data necessary for deriving the additional coefficient.
The Arrhenius relationship relates the decay-rate coefficient at TC °C to that at a reference temperature, which we nominated as 20°C. Then
kTC = TCOEF*k20
where TCOEF is defined in the procedure below. TCOEF is a function of the additional parameter EOR, which is estimated simultaneously from decay-test data with the decay coefficients at 20°C (denoted KF20 and KS20 below).
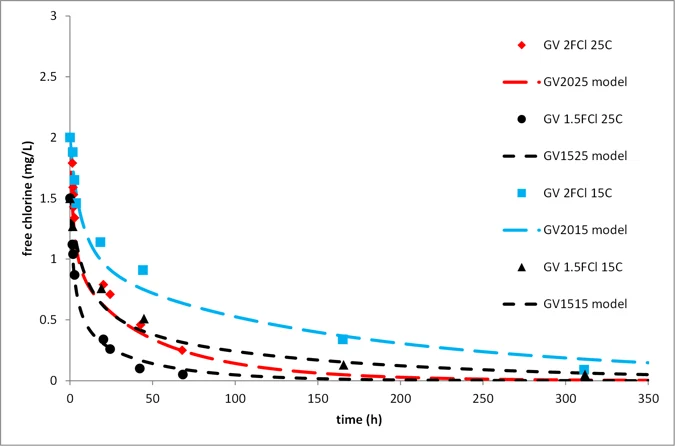
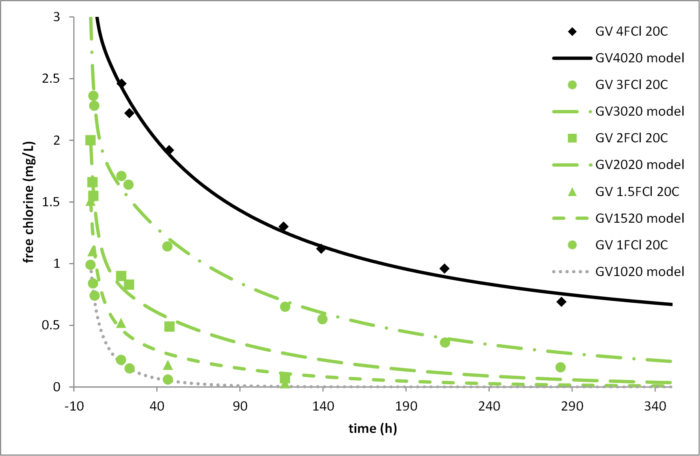
Figure 2 compares the decay-test data for Greenvale water at 15, 20, and 25°C with predictions from the 2RA model, using coefficient values derived from only the three curves shown in black.
Figure 2. Comparison of decay-test data (points) at various temperatures for Greenvale water with 2RA model predictions (curves). Only filled black points were used for model calibration.
These five coefficient values are inserted in the augmented 2R model specified in the MSX format below. Only the [TITLE] and [COEFFICIENTS] sections need to be modified to specify the 2RA model. Any water temperature (TC) can be specified. Ideally, TCOEF, KF, and KS could then be calculated by the software before the simulation begins, but this is not possible in MSX at present. To avoid these calculations occurring at every time step, it is best to do them offline, as indicated in the procedure below.
[TITLE]
Augmented two-reactant (2RA) model of chlorine decay in bulk water at any temperature (Fisher et al. 2012)
[COEFFICIENTS]
; Type Name Value
; Specify decay coefficients at 20C and temperature coefficient EOR
CONSTANT KF20 0.164 ; Fast rate coefficient at 20°C [L/mg/h]
CONSTANT KS20 0.00496; Slow rate coefficient at 20°C [L/mg/h]
CONSTANT EOR 10500 ; (Activation energy E)/(gas const. R) [K]
;
CONSTANT TC 26.5 ; specify any simulation water temperature [degC]
; calculate TCOEF, KF, and KS offline for computational efficiency
CONSTANT TCOEF 2.177 ; TCOEF = exp [EOR*(TC-20)/(20+273)/(TC+273)]
CONSTANT KF 0.357 ; Fast rate coefficient at TC [L/mg/h] {=KF20*TCOEF]
CONSTANT KS 0.0108 ; Slow rate coefficient at TC [L/mg/h] {=KS20*TCOEF}
Table 2. Modifications required to convert 2R model of Table 1 to a 2RA model
We have found no case which requires more than two reactants or more than a single set of five coefficients to represent chlorine reactions accurately and efficiently in a given water overall operating conditions, including different temperatures.
How are the Coefficient Values for the 2R Model Derived from Decay Tests?
Conducting a decay test is well described in the Wiki https://bentleysystems.service-now.com/community?id=kb_article_view&sysparm_article=KB0057448 with the extra requirement that they should be conducted at constant temperature (within ±1°C).
The 2R/2RA coefficients for Greenvale water in Tables 1 and 2 were derived by Fisher et al. (2011) and Fisher et al. (2012), respectively. These were derived from the decay tests shown in Figures 1 and 2 using the AQUASIM software, available free at https://www.eawag.ch/en/department/siam/software/.
Although AQUASIM is a flexible package for creating dynamic models and estimating their coefficients, it takes time to become familiar with its useful features.
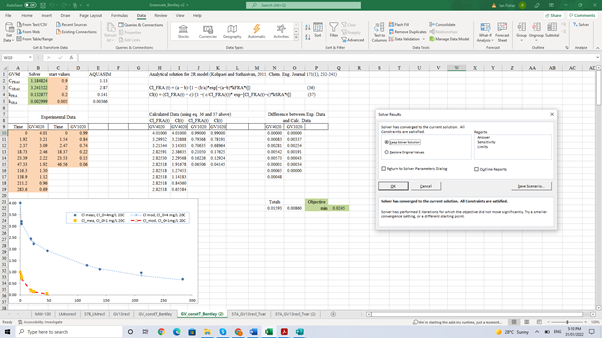
A simpler method to derive the coefficient values uses the Solver routine available in Excel (Figure 3). Data from the decay tests is first loaded into an Excel spreadsheet (orange cells starting at A10) and initial guesses of the coefficients (orange cells C2 to C5). The approximate solution for the 2R model (Kohpaei and Sathasivan 2011) is used to predict chlorine at the same times (starting at cell H10). The coefficient values are then optimized by Solver to minimize the error between model predictions and data points. Non-negativity constraints are specified for each coefficient. Figure 3 also compares the data and 2R model predictions for the two Greenvale decay tests at 20°C shown in Figure 1 as full black lines. The optimal coefficient values obtained from the Solver run are shown in green cells B2 to B5.
Figure 3. Decay test data and 2R model predictions from coefficients estimated from the analytical solution of Kohpaei and Sathasivan (2011) and Solver optimization in Excel spreadsheet.
The coefficient values obtained from Solver are slightly different from those obtained from AQUASIM, but the predictions are of similar accuracy. This illustrates that the combination of the four coefficient values is important, not the absolute value of any one of them.
There is also no such thing as a typical set of coefficients because different waters can contain a wide variety and combination of substances (and concentrations) that react with chlorine. Consequently, the combination of coefficient values that best describes bulk decay in any water can only be derived from appropriate decay-tests.
Further Information and Assistance with the 2R and 2RA Models
The 2R and 2RA models have been developed and applied to numerous distribution systems over more than 20 years. Detailed information is contained in the journal articles listed below. A framework for using the models (with an associated wall-decay model) to find cost-effective chlorination strategies is also listed (Fisher et al. 2018).
Model originators, Ian Fisher and George Kastl, are members of the Western Sydney University Water Group, led by Dr. Arumugam Sathasivan, Professor of Water and Environmental Engineering, within the School of Engineering, Design and the Built Environment.
The Group would be pleased to assist water utilities in applying these models to their specific distribution systems by advising on, or conducting, the appropriate decay tests and the derivation of coefficients from them. Please note, after a preliminary scoping discussion, the costs of staff time and resources involved need to be covered by the client.
For a preliminary discussion, please email: [email protected] or [email protected]
References
Fisher, I.; Kastl, G.; Sathasivan, A., (2011). Evaluation of suitable chlorine bulk-decay models for water distribution systems. Water Research 45(16), 4896-4908.
Fisher, I; Kastl, G; Sathasivan, A., (2012). A suitable model of combined effects of temperature and initial condition on chlorine bulk decay in water distribution systems. Water Research, 46(10), 3293-3303.
Kohpaei, A; Sathasivan, A., (2011). Chlorine decay prediction in bulk water using the parallel second order model: An analytical solution development Chem. Eng. Journal 171(1), 232-241.
Fisher, I., Kastl, G., Shang, F., Sathasivan, A., (2018). Framework for Optimizing Chlorine and Byproduct Concentrations in Drinking Water Distribution Systems. Journal American Water Works Association 110(11), 38-49.
Want to learn more from our resident water and wastewater expert? Join the Dr. Tom Walski Newsletter today!