Choose Area of Interest
SEARCH SOFTWARE
by Sam Chappell
by Sam Chappell
by Breda Kiely
by Sam Chappell
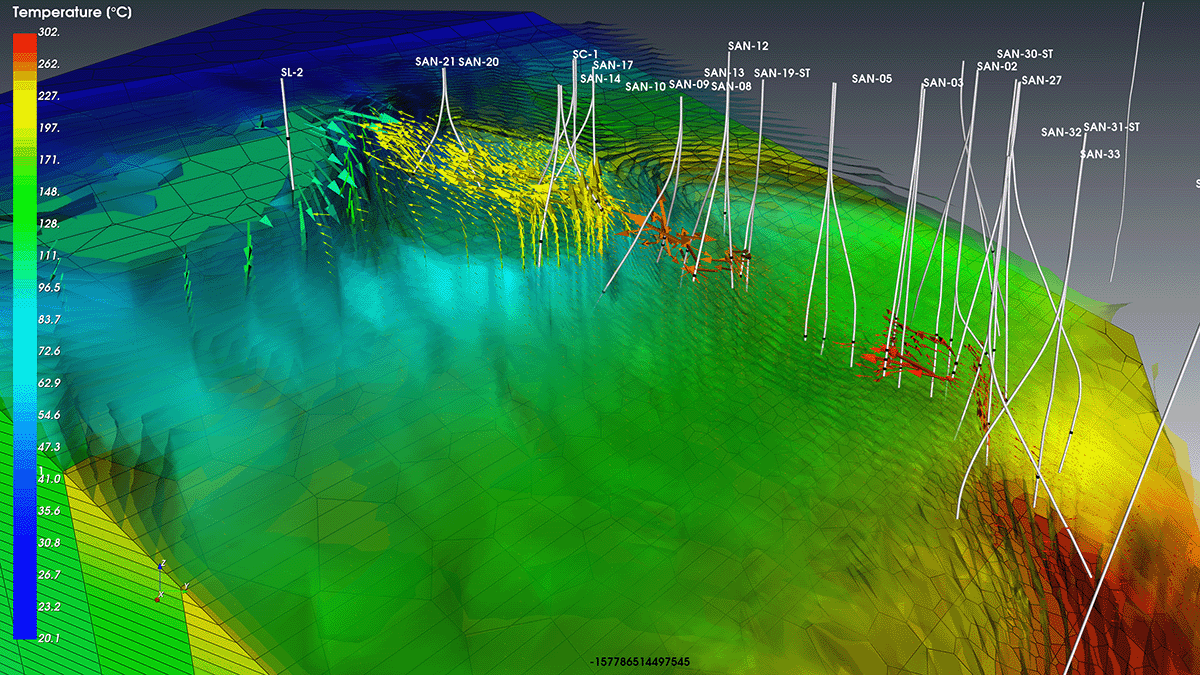
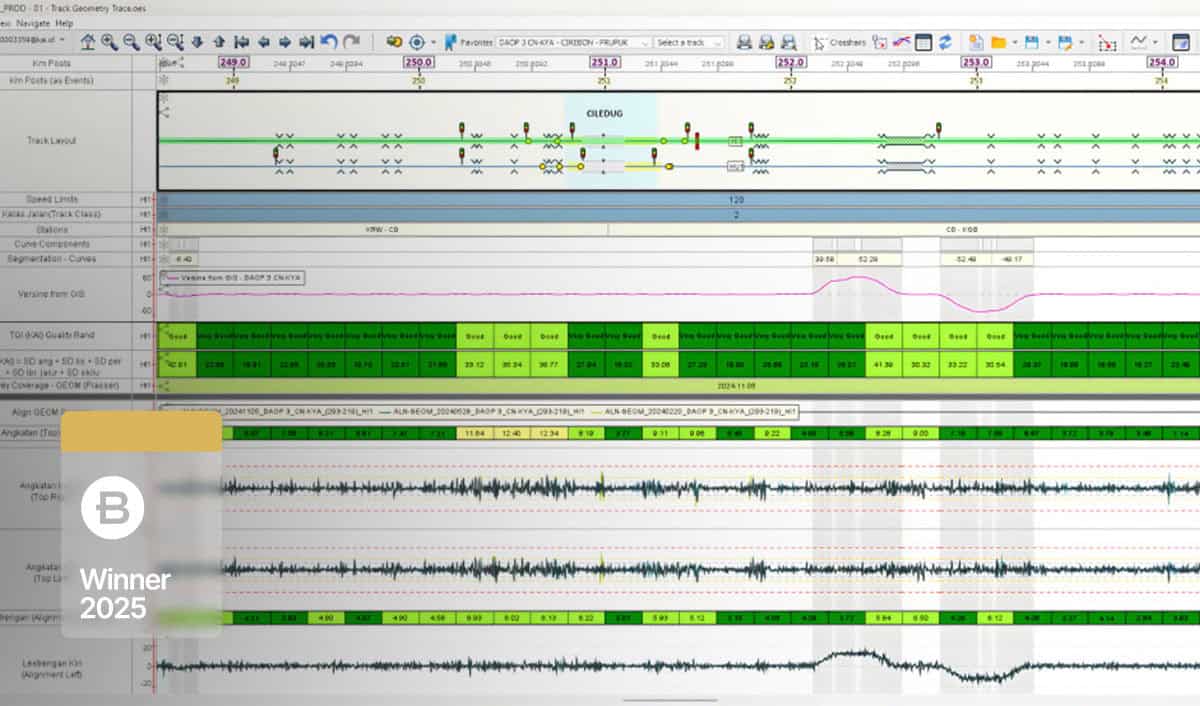
PT Kereta Api Indonesia’s AI–Powered Predictive Maintenance Transformation Organization: PT Kereta Api Indonesia (Persero) Project Name: Smart Predictive Maintenance and Digital Transformation of Indonesia’s Rail Network Location: Indonesia (7,000 kilometers of national rail network) Project Phase: Completed (digital transformation in...
by Breda Kiely
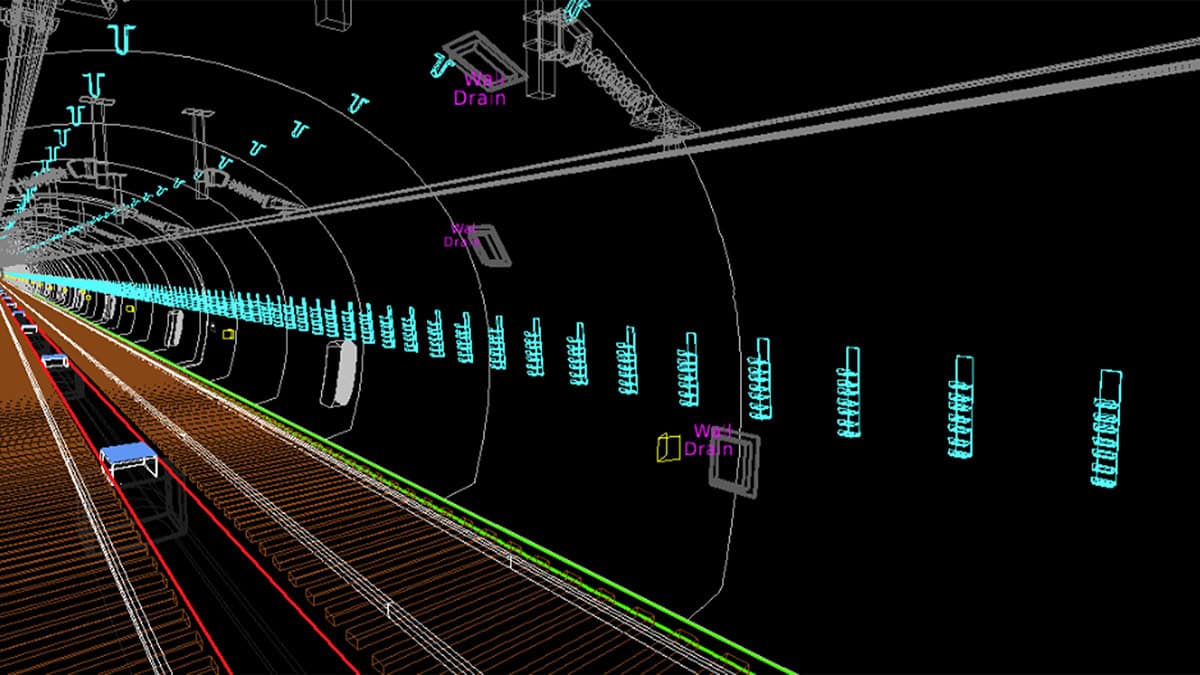
Network Rail’s Digital Twin of the Historic Severn Tunnel Organization: Network Rail Project Name: Severn Tunnel Digital Twin – Enhancing Rail Asset Management Location: Severn Tunnel, United Kingdom (linking England and Wales) Project Phase: Completed (digital twin in operational use)...
by Breda Kiely
PT WIKA Tirta Jaya Jatiluhur’s Digital Transformation of West Java’s Regional Clean Water System Organization: PT WIKA Tirta Jaya Jatiluhur (WTJJ) Project Name: SPAM Regional Jatiluhur I – Transforming Water for a Better Tomorrow Location: West Java, Indonesia (serving Jakarta,...

by Neda Simeonova
Empresas Públicas de Medellín’s Digital Model–Driven Water Network Transformation Organization: Empresas Públicas de Medellín (EPM) Project Name: Integrated Digital Modeling of Medellín’s Primary Aqueduct Network Location: Medellín, Colombia Project Phase: Completed and Operational Estimated Project Cost: USD 100 million Bentley...

by Neda Simeonova
The Atal Puram Township Project Organization: Voyants Solutions Private Ltd Project Name: The Atal Puram Township Location: Kakua–Bhandai villages in Agra, India Project Phase: Design Expected Completion Date: March 14, 2027 Estimated Project Cost: INR 413 Crores ($47 million USD)...

by Tye Masters